If you have been reading about blockchain networks like Bitcoin and Ethereum, you must have come across the term "Proof-of-work" (PoW). Most of the blockchain enthusiasts will tell you that PoW is a consensus mechanism using which miners solve complex mathematical puzzles to produce blocks. Buy WHY? Why do they need to solve complex mathematical puzzles to produce blocks? Why can't a node simply bundle a bunch of transactions and broadcast to the network?
I asked these questions repeatedly when I was reading up various blockchain concepts. Fortunately, I understood the "Why" part eventually. So, if you have the habit of questioning things and want to understand "why to solve mathematical puzzles to produce blocks" then you are at the right place.
Read on to find out.
Some rules
To understand why PoW is needed, you need to know some of the basic rules of a blockchain network. Let me outline them below:
- Every miner in the blockchain network maintains the entire blockchain in its local node.
- When a particular node wants to produce blocks, it bundles multiple transactions into a new block, adds it to the local blockchain and then broadcasts the message to other nodes in the network.
- When nodes receive the message about a new block, they compare the length of their own blockchain (A) with the one on the block-producer's machine (B). If the length of B is higher, they accept it and discard their local copy.
Scenario
Let's imagine a blockchain network where users can send each other a digital currency called "Hashnode Coin" (HCN). Assume that we have 4 nodes in the network - A, B, C, and D. Also, the current length of blockchain on all the nodes is 7.
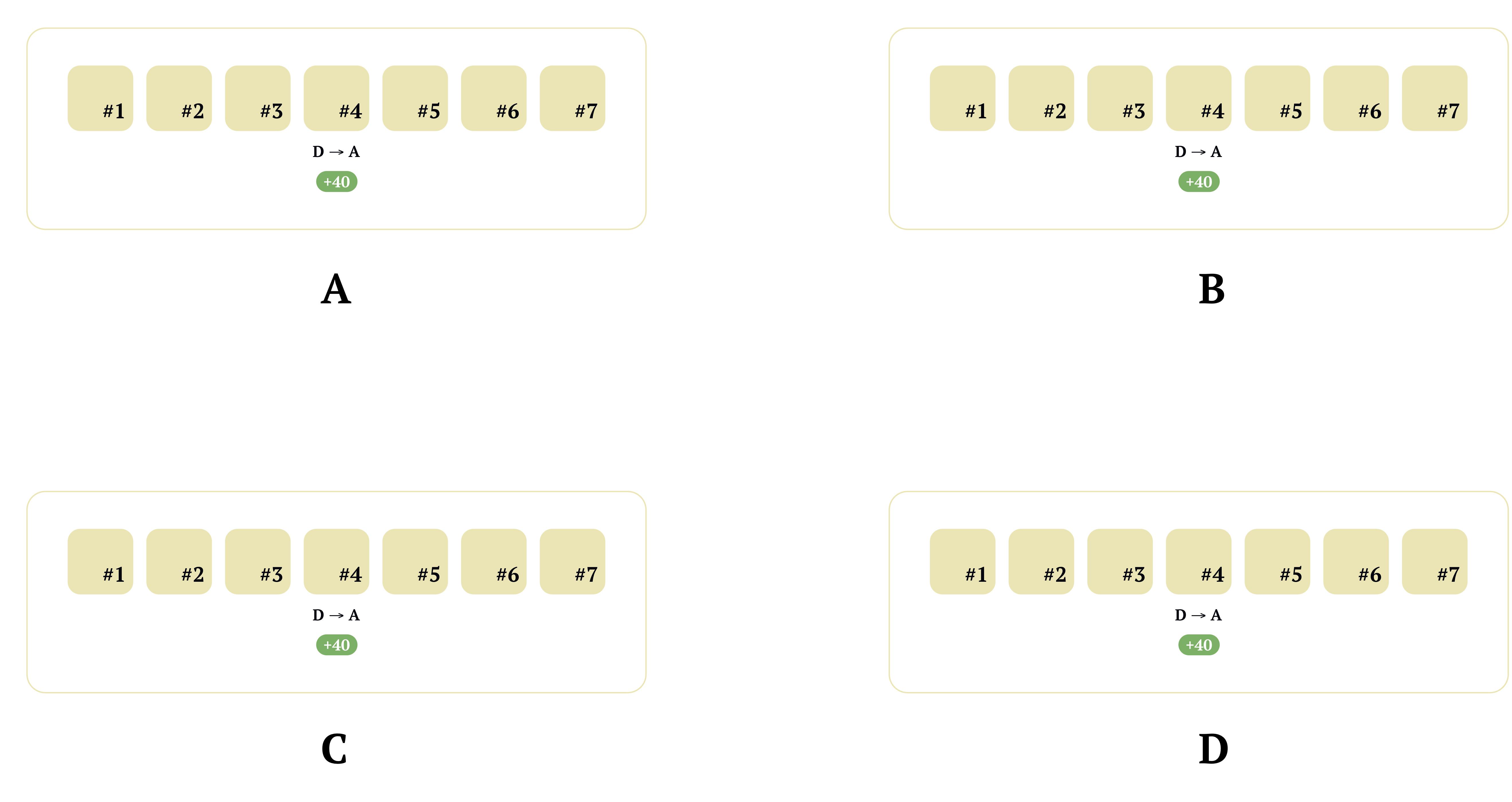
This system doesn't have any kind of consensus mechanism. If I need to produce a block, I just add it to my local copy and broadcast the message.
Note that D has sent 40 HCNs to A and this particular transaction is a part of the 4th block. Now assume that D wants to go rogue and wants to tamper with the blockchain by erasing its 40 HCN transaction to A. How would D achieve this?
Solution
D knows that the longest chain wins. She also knows that every block stores the hash of the previous block. So, she can't directly remove her transaction from the 4th block. That's why she carefully crafts the following strategy to remove her transaction from the blockchain:
Firstly, D removes block number 5, 6 and 7. This is because if she tampers with the 4th block, its hash changes and the subsequent blocks become invalid as they point to incorrect hash now.
D removes her transaction from 4th block.
Next, she bundles a bunch of incoming transactions, creates three new blocks and adds them after the 4th block. These new blocks form block no. 5, 6 and 7.
As of now the length of blockchain in all of the nodes is still equal (which is 7). D adds one more block to its copy to make its blockchain longer than others' copies and broadcasts the message.
When other nodes receive the message and see that D's blockchain length is more than theirs, they accept the copy and discard their own local version.
As a result, D is able to successfully tamper the blockchain by erasing one of its transactions from the history.
Enter PoW
Now let's assume that every member of the network has to solve a difficult mathematical problem if they want to propose blocks. For example, let's say D (and everyone else) has to find a number whose md5 hash has 4 leading zeroes in order to produce blocks. This is a very difficult task and you have to do trial and error for a long time to find your desired number. But once you find your number, everyone can calculate its md5 hash and verify that it actually has 4 leading zeroes. As it takes significant computing power to find the magic number, this proves that the node has done sufficient work to produce the block.
Feel free to try this tool to find a number whose md5 hash has 4 leading zeroes. After a few attempts, you will realize that it's impossible to find such a number without high computational power.
Because of Proof-of-work constraint, D has to find the "magic number" 4 times in a row (before anyone else does) after erasing the transaction in the 4th block to successfully corrupt the blockchain. As you may have guessed, it's extremely unlikely. Proof-of-work makes it harder to produce blocks, thereby making it difficult for malicious users to corrupt the blockchain.
PoW has some serious drawbacks as well. First of all, it takes a lot of time to confirm transactions since miners compete to find out the magic number. Secondly, the hardware and equipment used by the miners consume a lot of electricity.
Due to this, newer blockchain networks are switching to better options such Proof of Stake, Delegated Proof of Stake, Proof of Authority etc. You can read about them here.
This was a quick answer to "Why is PoW important?". I presented a very simplified picture. In reality blockchain networks like Bitcoin have complex rules and protocols in place which makes it nearly impossible to tamper with the blockchain. However, the basic concepts are still the same. If you want to understand how the protocols work in production deployments, take a look at this.
If you enjoyed reading this article, feel free to join our telegram channel and let me know your questions in the comments below!