So what are graphs exactly ? lets see what Wikipedia has to say about graphs:

a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects correspond to mathematical abstractions called vertices (also called nodes or points) and each of the related pairs of vertices is called an edge (also called an arc or line)

vertices = nodes.

So if we summary things up a graph is a structure with Nodes and Edges.

Here is an example of simple graph with Nodes & edges.

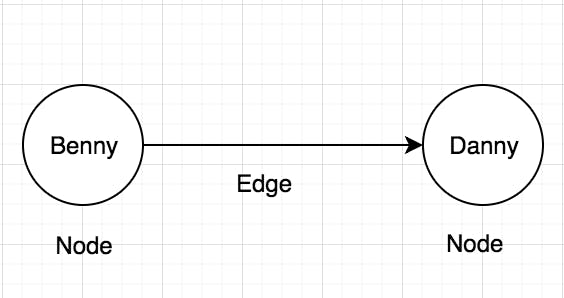
from this simple graph we can understand 1 thing, Benny knows Danny. there are 2 types of Graphs direct and undirected.

the above example is direct graph, Benny's is "following" Danny but Danny is not.

Undirected graph of the above example will look like this:

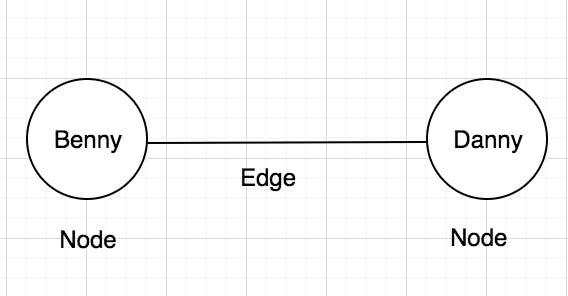This means that Benny's is "following" Danny and Danny's "following" Benny.

So What is BFS algorithm and when can I use it ?

Breadth-first search algorithm

BFS is a search algorithm which can be applied only on graphs. bfs can answer on 2 questions:

1. There is a path from Node A to Node B ?
2. What is the shortest Path from Node A to Node B ?

Lets answers both of those questions in more detail:

1. There is a path from Node A to Node B ?

Suppose you have a facebook account and you have some friends in it (I hope you have few ;) and you want to look for a friend which knows a person with the name 'Gorge'.

An illustration of that kind of graph

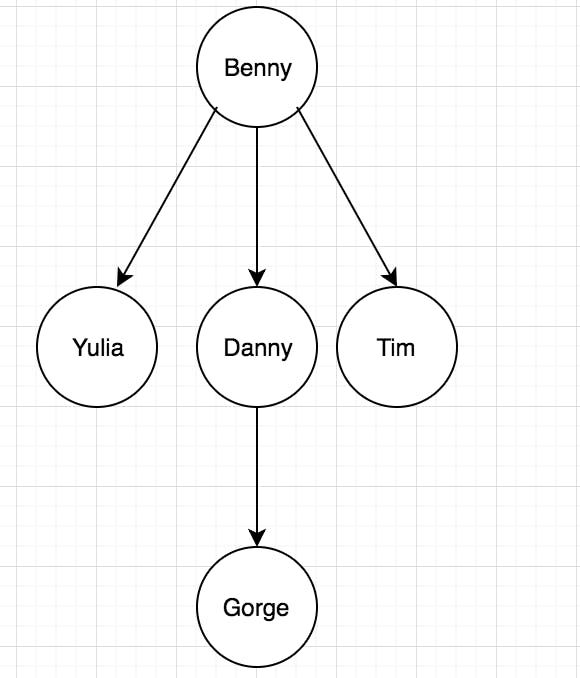
As we can see Benny has 3 friends :) (Yulia, Danny & Tim) Danny knows Gorge and this is the guy I was looking for. but how I can implement this?

One way to implement it is just making a list of all of my friends and check if any of my friends has a friend called 'gorge'

If you don't know any gorge, you will have to check inside your friends friends and see if they know any 'Gorge' each time you search for 'gorge' if the person you checked is not gorge you add all of his friends to the list until you find 1 person called 'Gorge'.

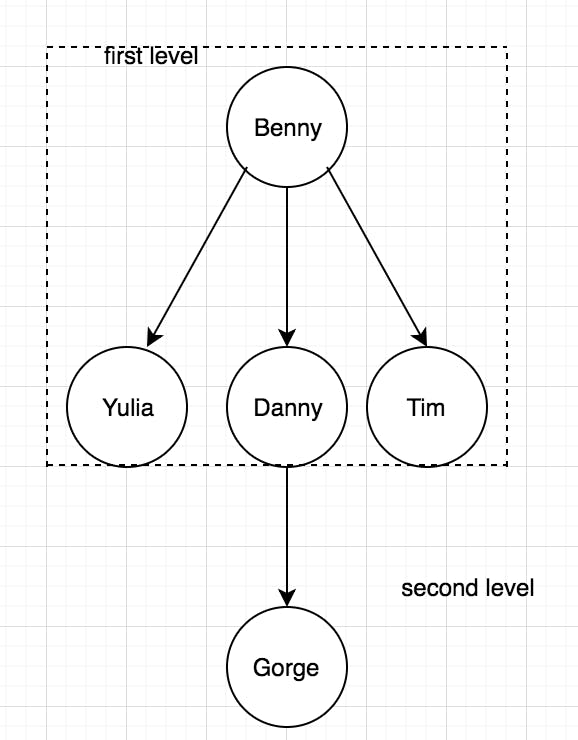
So lets change the question to fit our problem:

1. There is a path from Node A to Node B ?
2. There is a person called 'Gorge' linked to me in a certain way on facebook ?

BFS search by levels = Better to find 'gorge' as it's my friend first (first level) than a friend of a friend. (second , third ... level)

So how can we put them in such order the search by the friend level?

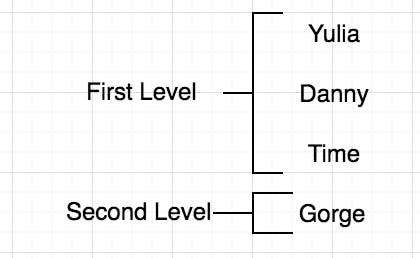
The best data structure for this algorithm is of course 'Queue' which means [First In First Out] or in short FIFO.

Assuming you are waiting at the line to pay at the supermarket ( and they don't have automatic cashier to do it yourself ;) ) the one enter first is the first in line to pay and exit the super.

this is exactly what we need here right? if we "throw" this solution to our needs: The person we are looking from is the person we want to star checking all of his friends.

So we start with me: 'Benny' and take all of my friends. check each one of them, if they don't 'Gorge' they are added to the queue. this way we validate that we first check these who enter first.

We dequeue to take from the bottom of the queue and enqueue to add the person to the top of the queue.

Implementation

So how do we implement this? lets draw our example in some python code.

graph = {}
graph["Benny"] = ["Yulia", "Danny", "Tim"]
graph["Danny"] = ["Gorge"]
graph["Yulia"] = []
graph["Tim"] = []

That's it, we wrote our first graph which demonstrate the image above with all its relations.

Benny following Yulia, Danny & Tim Danny following Gorge Yulia just registered and don't following anyone yet Tim too.

import queue
lookup_queue = queue.Queue()
graph = {}
graph["Benny"] = ["Yulia", "Danny", "Tim"]
graph["Danny"] = ["Gorge"]
graph["Yulia"] = []
graph["Tim"] = []
graph["Gorge"] = []
lookup_queue.put(graph["Benny"])
def bfs(graph, person_to_find):
    checked = []
    while not lookup_queue.empty():
        peoples = lookup_queue.get()
        for p in peoples:
            if p not in checked:
                checked.append(p)
                if person_to_find in graph[p]:
                    return f"{p} knows him."
                else:
                    if graph[p]:
                        lookup_queue.put(graph[p])

    return None

print(bfs(graph, "Gorge"))

As you can see to avoid infinity loop of undirected paths (cases when Benny following Danny and Danny following Benny) we added a 'checked' list to add each person we looked for in-order to avoid putting them into the queue again.

If we were passing a person which are not found in any of my network connections then we would get None from the BFS function which means There is no path from me to this person, and of course if we don't have path we don't have shortest path either.

Running time

If we looking all of the person network for 'Gorge' so that means we follow each edge ( The Arrow in the illustrations above ) so running time is at least O(number of edges) but we also keep queue for every person, adding person is O(1). for every person is O(number of people) total. to summeries: O(number of people + number of edges) = O(N + E)

Feel free to ask any question you want!