The Art of Backtracking
Sudoku Solver - with Dynamic Programming
Backtracking is an algorithm that is often used for problems whose solutions are generated in stages and each new stage depends on the previous.
As soon as it determines a particular stage has no possible solution, it abandons it (backtracks) and goes to find a new solution for the previous stage consequently creating a new chance for a solution to be found for the stage that was backtracked.
For this code, the Sudoku grid is represented as a 9×9 array where '0' signifies an empty space in the grid.
Line-by-line explanation of Code
import numpy as np
import numpy as np imports the numpy library which is very useful for performing mathematical and logical operations on large high dimensional arrays and matrices.
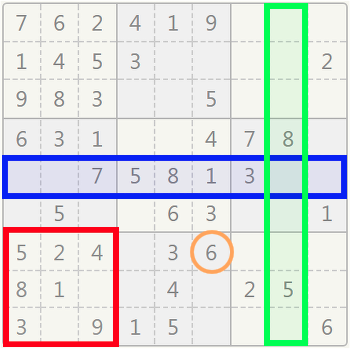
def check_row(row, char):
#Returns True if char not in row
if char in row:
return False
else:
return True
Function check_row takes in a row from the Sudoku grid and a character, then checks if the character already exists in that row.
The rectangle with blue outline represents an example of such row.
def check_column(matrix, char, pos):
#Returns True if char not in column
to_check = []
col = pos[1]
for i in range(len(matrix)):
to_check.append(matrix[i][col])
if char in to_check:
return False
else:
return True
Function check_column takes in the Sudoku matrix grid, a character and it's position (as coordinates), then checks if the character already exists in that column.
The rectangle with green outline represents an example of such column.
def check_box(matrix, char, pos):
#Returns True if char not in sectioned box
to_check = []
row, col = pos[0], pos[1]
start_row, start_col = (row//3)*3, (col//3)*3
for i in range(3):
for j in range(3):
to_check.append(matrix[start_row+i][start_col+j])
if char in to_check:
return False
else:
return True
Function check_box takes in the Sudoku matrix grid, a character and it's position (as coordinates), then checks if the character already exists in that box.
The square with red outline represents an example of such box.
The start row and column representing the box are gotten by performing a perfect division of 3 of the position(row,column) considered. The perfect divisions or quotients are then multiplied by 3 to get the start positions.
Example:
Initial position [2,3]
start_row = 0×3 = 0
start_col = 1×3 = 3
start position = [0,3]
This position represents '4' in the first row of the Sudoku grid image above.
def checker(row, matrix, char, pos):
boolean = check_row(row, char) and check_column(matrix, char, pos) and check_box(matrix, char, pos)
return boolean
Function checker takes in a row from the Sudoku matrix grid, the grid itself, a character and it's position (as coordinates) and returns True if it is a possible solution for that position.
def sudoku_solver(array):
"""
Function 'sudoku_solver' takes in a 9×9 array of numbers representing a Sudoku grid and returns a new grid with solution.
"""
options = range(1,10)
to_check = []
#Handling errors with input
if isinstance(array,list) and len(array)==9:
for list_ in array:
if isinstance(list_,list) and len(list_)==9:
for char in list_:
if char==0 or (char in options):
pass
else:
return "Invalid input."
else:
return "Invalid input."
else:
return "Invalid input."
These first few lines of the function sudoku_solver deal with errors from input so as not to interfere with the actual code.
options stores the values of possible solutions we can have for an empty space.
to_check stores the coordinates of the empty spaces in the Sudoku matrix grid to be filled.
#Gets all empty spaces in grid to be filled
for row in range(9):
for col in range(9):
if array[row][col]==0:
to_check.append([row,col])
These lines, as the comment says, gets all the empty spaces (represented as '0') in the grid to be filled storing them in the list to_check defined earlier.
i = 0
while i!=len(to_check):
try:
current_row = array[to_check[i][0]]
r,c = to_check[i]
current_char = array[r][c]
next_ = 0
These lines of code first established the variables (relating to the current empty space) to be used in processing.
current_row stores the row on which the current empty space being treated is.
r stores the position of its row in the grid.
c stores the position of its column in the grid.
current_char stores the value of empty space(0) or the solution bactracked to.
#Gets possible solution to empty space
try_ = options[current_char+next_]
#Checks if it satisfies its position and sets it
while not checker(current_row, array, try_, to_check[i]):
next_+=1
try_ = options[current_char+next_]
else:
array[r][c]=try_
i+=1
try_ stores the value of a possible solution for the empty space while looping through the options variable defined in the first lines of the function 'sudoku_solver'.
Its index current_char+next_ works like this.
next_ stores a value that shifts the index forward if a solution is not found.
Example:
If current_char is an empty space which is '0' and next_ is also 0, then the index for try_ is 0+0=0. which means '1' is picked as the first valid possible solution.
while not checker(current_row, array, try_, to_check[i]):
next_+=1
try_ = options[current_char+next_]
If '1' doesn't satisfy that position, meaning checker(current_row, array, try_, to_check[i]) returns False, next_ increases by 1 therefore shifting to '2' as the next possible solution.
If current_char was a number backtracked to, let's say 6, it means 1 to 5 had already been checked before and didn't satisfy that position.
So next_ being 0 (at first), means the new index is 6+0=6, therefore setting '7' as the next valid possible solution.
else:
array[r][c]=try_
i+=1
Once determined that a number is a valid possible solution, the empty space or position backtracked to is changed to that number and we move to the next empty space coordinate to be filled by increasing i by 1.
try:
...
except:
#If no possible solution was found, backtracks to find new solutions
array[r][c]=0
i-=1
The try block tests the code which should run smoothly unless current_char+next_ representing the index for the option variable is out of range.
If so, the except block is called to set that particular position to '0' if it isn't and then backtracks to the previous empty space coordinate filled by decreasing i by 1.
The initial while loop is then run, with the previous empty space set as the current.
return np.matrix(array)
This line of code returns our solved Sudoku matrix grid. Hurray!!
The directory containing the full code can be found here.
Visualising the Sudoku Solver with python's Tkinter, I designed this.